Appendix: Upwind scheme

Appendix: Upwind scheme#

강좌: 기초 전산유체역학

Modified Wavenumber Analysis for Upwind scheme#

PDE Solution을 \(u(x, t) = \psi(t) e^{ikx}\) 로 생각한다.

이를 아래 Upwind 차분식에 적용하면 다음과 같다.

\[ \frac{du(x_j, t)}{dt} = - a \frac{u(x_j,t) - u(x_{j-1}, t)}{\Delta x} \]
\[ \frac{d \psi}{d t} e^{ikx_j} = - \frac{a}{\Delta x} \left (e^{ikx_j} - e^{ik(x_j - \Delta x)} \right) \psi \]

이를 정리하면

\[ \frac{d \psi}{d t} = - \frac{a}{\Delta x} \left (1 - e^{-ik\Delta x} \right) \psi = -a i \frac{-i + i e^{-ik\Delta x}}{\Delta x} \psi = -a i k' \psi. \]

차분식에 의해 Modified wavenumber \(k'\) 은 다음과 같다.

\[ k' = \frac{-i + i e^{-ik\Delta x}}{\Delta x} \]

Stability 분석을 위해 모델 방정식 형태로 표현하면 \(\lambda=-iak'\) 를 분석하면 다음과 같다.

\[ \lambda = - i a k' = - \frac{a}{\Delta x} \left (1 - e^{-ik\Delta x} \right) \]

Central 기법과 달리 복소수이다.

Stability Region#

앞서 구한 몇가지 ODE 에서 Stability region은 다음과 같다.

Euler Explicit#

\[ \sigma = 1 + z \]

4차 정확도 Runge Kutta Method#

\[ \sigma = 1 + z + \frac{1}{2} z^2 + \frac{1}{6} z^3 + \frac{1}{24} z^4 \]

여기서 \(z=\lambda \Delta t\) 이다.

앞서 구한 \(\lambda\) 를 이용해서 분석하면 다음과 같다.

\[ z = \lambda \Delta t = -\frac{a \Delta t}{\Delta x} \left (1 - e^{-ik\Delta x} \right) = -\nu \left (1 - e^{-ik\Delta x} \right) \]

이 경우 대부분 실수 측에서 Stability 한계가 결정된다.

이를 확인하기 위해 수치적으로 \((\nu, k \Delta x)\) 에 대해 극좌표게로 분석 가시화 해본다.

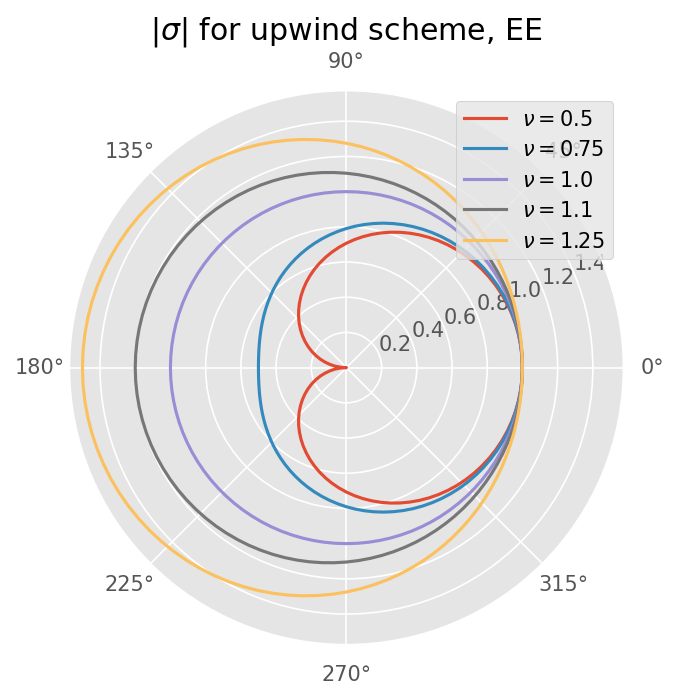
Euler Explicit#

Von nuemann 안정성 분석과 동일한 결과이다.

  • 실수측 \(k \Delta x = 0, 180\) 일 때 \(\sigma\) 가 최대이다.

  • \(Real(z)\) 대해서만 분석하면

\[ Real(z) = -\nu (1 - \cos(k \Delta x)) \]

즉

\[ \min(Real(z)) = - 2 \nu \]

  • Euler Explict의 최대 실수측 범위인 -2를 고려하면

\[ \nu \leq 1. \]
%matplotlib inline
from matplotlib import pyplot as plt

import numpy as np

plt.style.use('ggplot')
plt.rcParams['figure.dpi'] = 150

theta = np.linspace(0, 2*np.pi, 101)
fig, ax = plt.subplots(subplot_kw={'projection': 'polar'})

nus = [0.5, 0.75, 1.0, 1.1, 1.25]
for nu in nus:
    z = -nu *(1 - np.exp(-theta*1j))
    
    # Amplication factor for EE
    sigma = 1 + z
    ax.plot(theta, abs(sigma))

ax.legend([r'$\nu={}$'.format(nu) for nu in nus])
ax.set_title(r'$|\sigma|$ for upwind scheme, EE')

Text(0.5, 1.0, '$|\\sigma|$ for upwind scheme, EE')
../_images/7e3b193b35b6646a5dd4ac31fc2b7bba3bdfd4c81c0b713f6ab8b466fa02e653.png

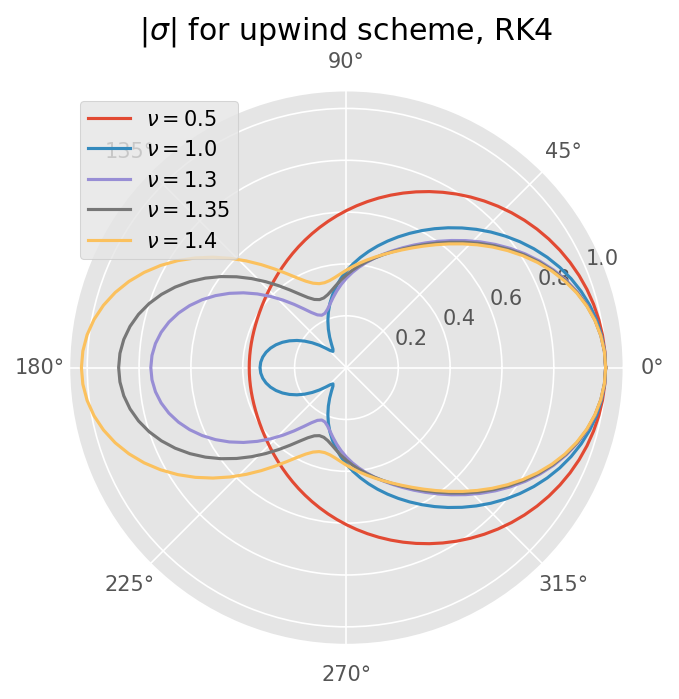
4차 정확도 Runge Kutta Method#

Von nuemann 안정성 분석과 동일한 결과이다.

  • 실수측 \(k \Delta x = 0, 180\) 일 때 \(\sigma\) 가 최대이다.

  • \(Real(z)\) 대해서만 분석하면

\[ \min(Real(z)) = - 2 \nu \]

  • Euler Explict의 최대 실수측 범위인 -2.79를 고려하면

\[ \nu \leq 1.395. \]
theta = np.linspace(0, 2*np.pi, 101)
fig, ax = plt.subplots(subplot_kw={'projection': 'polar'})

nus = [0.5, 1.0, 1.3, 1.35, 1.4]
for nu in nus:
    z = -nu *(1 - np.exp(-theta*1j))
    
    # Amplication factor for RK4
    sigma = 1 + z + 0.5*z**2 + z**3/6 + z**4/24
    ax.plot(theta, abs(sigma))

ax.legend([r'$\nu={}$'.format(nu) for nu in nus])
ax.set_title(r'$|\sigma|$ for upwind scheme, RK4')

Text(0.5, 1.0, '$|\\sigma|$ for upwind scheme, RK4')
../_images/b7941b654fabf479f86b751f1f8435d16b6456ad5fb494a61c3c6b334ad9a59b.png
Contents